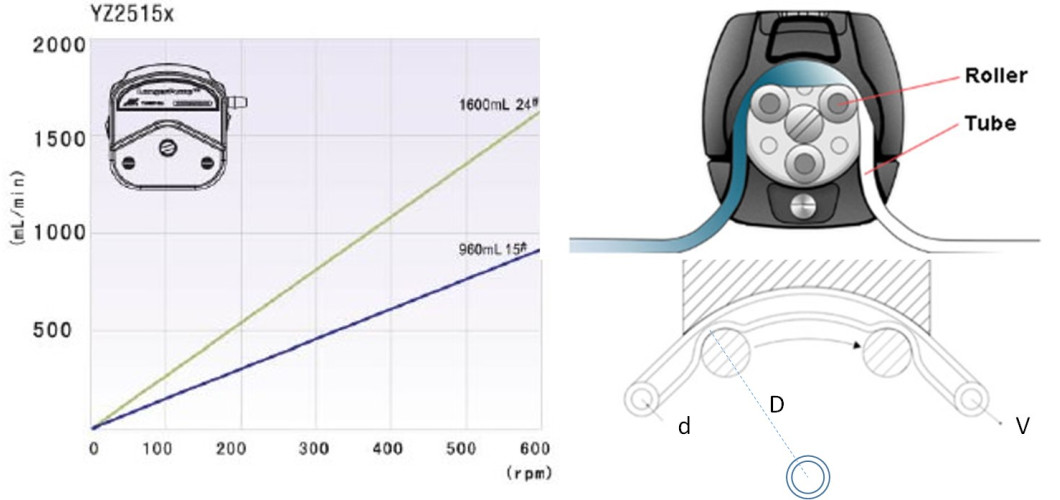
The flow rate of a specific peristatic pump is determined by three major parameters: the rotation speed (N rpm) of the rotor shaft, the inner diameter (d cm) of the hose, and the diameter (D cm) of the roller assembly. The flow rate V (mL/min) can be expressed in the following formula.
V = [p (d/2)2] [p(D+2T-d)b]N
Where T is the wall thickness of hose in cm (centimeter), which is usually much smaller than D, and b is the effective fraction for a cycle of rotor rotation. The flow rate formula above indicates the following general conclusions under normal run conditions:
- The volume flow rate is proportional to the rotor speed N.
- The volume
flow rate is proportional to the square of the hose diameter.
- The volume
flow rate is closely proportional to the diameter of the roller track arc.
However, other factors need to be considered, since the
effective fraction b is
dependent on the number of rollers and roller diameters, the back pressure of
the inlet side (hose diameter and length, viscosity of fluid, and hose
material, etc.), and the rotation speed N when N is too big.
As a numerical example, we can consider a system when being operated at N = 10 rpm; suppose the tubing inner diameter is d = 0.48 cm, wall thickness 0.16 cm, and the diameter of the roller assembly D = 4.0 cm, and b = 0.8 (typically b in the range of 0.6-0.8). So the flow rate is:
V = 3.14 x (0.48/2)2 x 3.14 x (4.0 +2x0.16- 0.48) x 0.8 x 10
= 17.46 mL/min
In application practice, the flow rate for a specific pump system should be calibrated, so a calibration curve can be plotted as shown in the following example. A simplified flow rate formula can be obtained:
V = kN
where
4 Comment(s)
Insightful and so easy to understand. I didn’t expect it to be this helpful.
10.0.0.1 provides easy access to router admin pages. This article explains login via 10.0.0.0.1, resolves common issues such as 10.0 0.1, clarifies confusion with 1.0.0.0.1, and guides users to manage WiFi passwords, firmware updates, connected devices, bandwidth control, and network stability.
This is a great breakdown of the mechanical variables involved in peristaltic flow—I especially appreciated the point about how fluid viscosity can cause the actual output to deviate from the theoretical calculation. Getting that "effective fraction" of rotor rotation dialed in is always the trickiest part of the process when you're aiming for precision. Thanks for simplifying the math; it’s going to save me a lot of trial and error in my own lab setup.
This is a clear and practical guide to calculating peristaltic pump flow rates. The formula breakdown with key parameters (N, d, D) is especially helpful for quick estimations. I appreciate the note about additional factors like back pressure and viscosity affecting the effective fraction b—often overlooked in simplified explanations. Thanks for sharing this useful reference!
Leave a Comment